Data Structure: Trie Tree
Here is an example of a Trie tree:
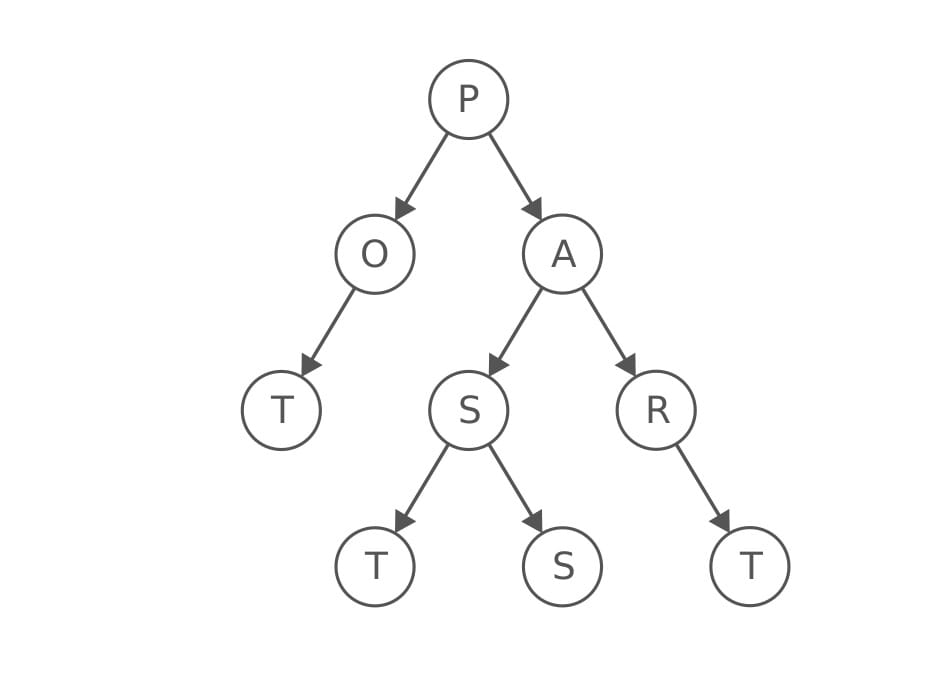Source interviewcake.com
It's a data structure used to store words and prefixes of words.
Note how the words are forming when you start from the root and go into the branches of the tree.
Look at the words PAST and PART, they share the same first nodes P and A.
This kind of data structre is very fast for word searching and word suggestions, it's like looking for a word in a dictionary, you don't go page by page and word by word, right? you'd open the page that has the first character of the word you are looking for, and then you try to look around for words that has the second character and so on until you find the word you are looking for.
Let's build it using python:
First, as you can see the tree is not binary, so each node can have multiple children nodes. The question is how shall we attach them to the parent node? as a list or as a dictionary?
Since we don't care about the order of the attached children, we better use a dictionary for fast lookup O(1) vs O(n) at each character if we use a list (which would result in a time complexity of O(nxm) where m is the length of the word we are looking for).
So, here is how the node is represented
class Trie_Node:
def __init__(self):
self.children: dict = dict()
self.is_word_end = False
Note that I've added a flag (is_word_end) to let me know when we have reach the end of a word in our tree.
Source interviewcake.com
Looking at the above example again, PA is not a word but PART is, therefore, we would have the flag as True at the node with the character T
Here is how I've implemented the whole Trie tree:
class Trie_Node:
def __init__(self):
self.children = dict()
self.is_word_end = False
class Trie_tree:
def __init__(self):
self.root = Trie_Node()
def insert(self, word: str):
'''Converts an input word into nodes in our Trie tree'''
# start at the root node
current_node = self.root
# loop over the word character by character
for c in word:
if not c in current_node.children:
# If this character is not in our tree:
# Create a node if it does not exist
current_node.children[c] = Trie_Node()
# Then switch to it
current_node = current_node.children[c]
else:
# If this character is already in our tree:
# Switch to it's node, and continue
# the looping over the remaining characters
current_node = current_node.children[c]
# set the last node (character) as a word end
current_node.is_word_end = True
return self
Let's harness it's powers!
So far we have the script that we will use to build our trie tree. Now, let's have some example use cases:
-
Searching
A user types a word and we search for it in our trie tree.
We return True if it's in our tree and False otherwise.
def lookup(self, word):
current_node = self.root
# loop over the word string character by character
for char in word:
# return false if we reached a character that is not in our tree
if not char in current_node.children.keys():
return False
# traverse to that child node
current_node = current_node.children[char]
return True
Let's test it:
my_trie = Trie_tree()
res = my_trie.insert("hello")
res = my_trie.insert("her")
res = my_trie.insert("car")
print(res.lookup("car")) # True
print(res.lookup("cat")) # False
print(res.lookup("ca")) # True
Note that searching for "ca" returns True which is wrong, it's part of a word, but not A word. So let's fix that:
def lookup(self, word):
current_node: Trie_Node = self.root
# loop over the word string character by character
for char in word:
# return false if we reached a character that is not in our tree
if not char in current_node.children.keys():
return False
# traverse to that child node
current_node = current_node.children[char]
# if it's a word (not part of a stored word), this will return True, otherwise: False
return current_node.is_word_end
Note the last line, this will make sure that we return True only when the whole word is stored in our tree.
Now if we run our test again:
print(res.lookup("car")) # True
print(res.lookup("cat")) # False
print(res.lookup("ca")) # False
That's better!
The fun part :)
How about we test our trie tree with a massive dataset?
First I'd like to test searching with normal for loop:
start = time.perf_counter()
for item in data:
if item == "Spb7I8yn":
print(True)
break
end = time.perf_counter()
print(end - start) # 0.016 second (16 milli seconds)
Now with the python built in in statement
start = time.perf_counter()
print("Spb7I8yn" in data)
end = time.perf_counter()
print(end - start) # 0.0048 second (4.8 milli seconds)
Now our trie tree
my_trie = Trie_tree()
for word in data:
my_trie.insert(word)
start = time.perf_counter()
result = my_trie.lookup("Spb7I8yn")
print(result)
end = time.perf_counter()
print(end - start) # 0.00047 second (0.47 milli seconds)
If we campare it with the optimized built it in, we can see that it's about 10 times faster!
The time complexity for lookup is O(length of the word) which is great!
But, maybe you're wondering, what about this step:
for word in data:
my_trie.insert(word)
But it's a one time step, so imagine we have a real world system in which we have our data in a Trie tree. We'd load the data once into our tree and that's it.
When we need to add another word to our tree then we would of course use the .insert method which is definitly more expensive that a .append method in a list.
Also, as of everything in the world, there is a tradeoff for having such a speed, which is the space complexity of O(n) where n is all of the characters of the stored words in our tree. For every character/node we are consuming more memory compared to having the character as an item in a list.